こんにちは、あぶちゃです。
このブログでは、AI業界への転職を考えている方に役立つ情報をお届けしています。転職に役立つヒントから最新のAIツールや技術の紹介をしています。本ブログによって、少しでもAIの魅力を感じていただけると嬉しいです!
 悩んでいる人
悩んでいる人ユークリッド距離ってなに?Pythonでユークリッド距離を計算する方法を知りたい!
以上のような疑問にお答えしていきます。
- ユークリッド距離とはなにか?
- numPyを使って、ユークリッド距離を計算する方法
- SciPyを使って、ユークリッド距離を計算する方法
データ分析や機械学習において、データ間の距離を求めることは非常に重要です。
その中でもユークリッド距離は最も基本的な距離の一つで、簡単に計算することができます。Pythonを使ってユークリッド距離を計算する方法を学んでみましょう。
本記事では、ユークリッド距離について解説した後、numPyとSciPyの2つの方法でユークリッド距離を計算する方法について解説しています。
それぞれの方法の使い方について、pythonコードを交えて詳しく解説します。
以下の記事では、AI職種を6つ紹介しています。未経験からでも転職は可能なので、AIに興味がある方は参考にしてみてください。


ユークリッド距離の求め方
ユークリッド距離とは?
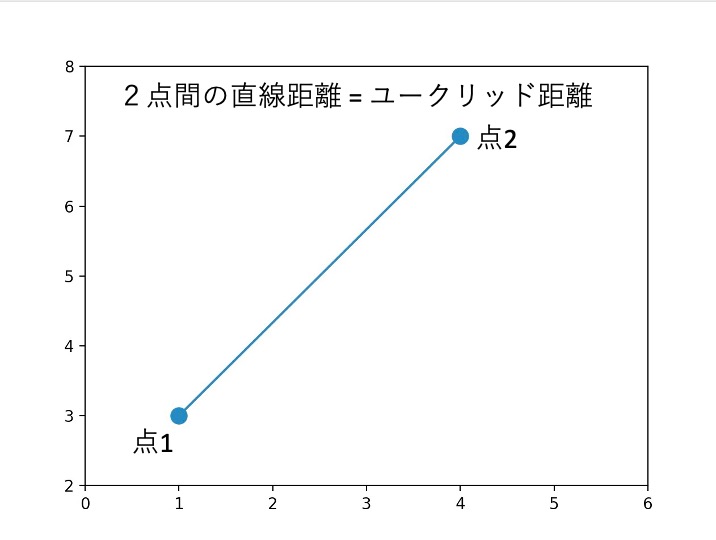
ユークリッド距離は、2つの点の間の直線距離を表す数学的な概念です。
2点間の距離を求める際に一般的に使用される距離のことであり、例えば、定規で測ったときの距離や地図上での2つの都市間の直線距離のことを指します。
少し難しく聞こえるかもしれませんが、みなさんが”距離”と聞いてイメージするであろう距離を数学的にユークリッド距離というだけです。
ユークリッド距離は、2つの点の位置を座標で示し、その2つの座標間の距離を求めることで計算できます。

ユークリッド距離の活用分野
ユークリッド距離は、距離の概念が必要なあらゆる分野で使用されていますが、機械学習にもよく使われます。
例えば、分類問題において、2つのデータポイントの距離を計算することで特徴量の類似性を測ることができます。
また、画像処理においても、2つの画像間のピクセル間の距離を計算することで、それらが類似しているかどうかを判断することができます。
一般的な概念ですが、機械学習においてもとても重要になるので、ここでしっかりと理解しておきましょう!
ピタゴラスの定理 (三平方の定理)【事前知識】
ピタゴラスの定理 (三平方の定理)とは?
ユークリッド距離を計算するために、ピタゴラスの定理を使いますので、事前に確認しておきましょう。
ピタゴラスの定理は、直角三角形の斜辺の長さを、残りの2辺の長さから求めるための基本的な定理です。
ピタゴラスの定理 : \(\displaystyle c^2 = a^2 + b^2\)
斜辺の長さを求めるために式を変形すると、
\(\displaystyle c = \sqrt{a^2 + b^2}\) となる。
斜辺の長さの2乗は、残りの2辺の長さa,bをそれぞれ2乗した数の和に等しいという式になります。
ピタゴラスの定理 計算例
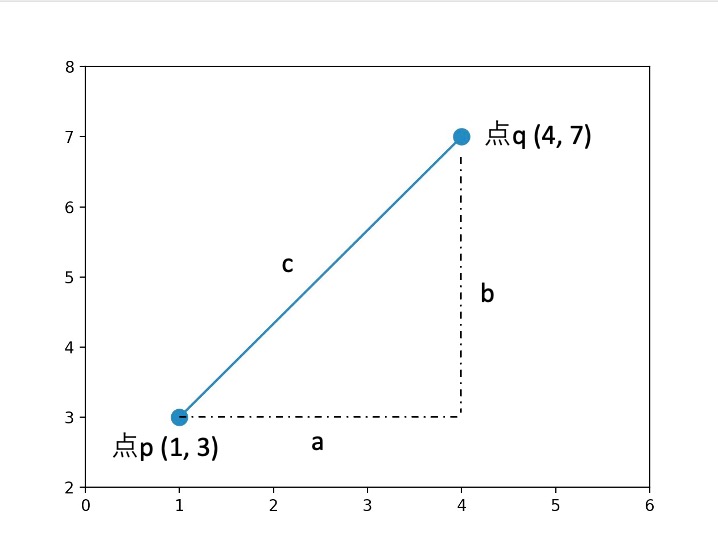

2つの点の座標位置を\(\displaystyle p = (1, 3), q = (4, 7))\) とした時の直角三角形の斜辺の長さを求めます。
まずは、斜辺以外の辺の長さを2点の座標から求めると、\(\displaystyle a = 4 – 1 = 3, b = 7 – 3 = 4\) となります。
算出したa、bを用いるとピタゴラスの定理より、斜辺の長さは\(\displaystyle c = \sqrt{3^2 + 4^2} = 5\) と計算できます。
ユークリッド距離の算出方法
ユークリッド距離とは、2つの点の間の最短距離でした。
上記のピタゴラスの定理の例では、2つの点の座標はxとy軸の2次元の座標と仮定しましたが、数学的には3次元空間や、さらに高次元空間においても同様に距離を求めることができます。
そこで、n次元空間を考えたとき、2つの点p, qの座標は、\(\displaystyle p = (p_1, p_2, \cdots, p_n), q = (q_1, q_2, \cdots, q_n)\)と定義できます。
\(ユークリッド距離 = \sqrt{\displaystyle \sum_{k=1}^{n}(q_i – p_i)^2}\)
Pythonでユークリッド距離を計算する2つの方法
計算する2つの方法
Pythonでユークリッド距離を計算するのに、よく使われている方法として以下の2つの方法があります。
Pythonでユークリッド距離を計算する2つ方法
- numPyを使う方法
- SciPyを使う方法
この2つのライブラリを使用したユークリッド距離の計算方法を解説します。
numPyとSciPyの使い分け
ユークリッド距離を計算するために2つの方法がありますが、どちらを使うのが良いのでしょうか?
まずは、それぞれのライブラリがどういったものかを把握しましょう。
numPy、SciPyの概要
- NumPy:高速な数値計算を可能にするライブラリ。多次元配列や行列計算に強い。
- SciPy:科学技術計算のためのライブラリ。NumPyをベースにした機能の他に、最適化、信号処理、画像処理、統計解析などの機能が含まれている。
SciPyはたくさん機能が含まれていますがNumPyをベースとしたライブラリであり、ユークリッド距離を計算する限りにおいては、どちらのライブラリを使用しても変わりはありません。
2つの方法を両方とも解説します。自分に合う方法を使用してください。
ユークリッド距離の計算【numPyを使う方法】
使用するnumPyの関数
次の構文で、ユークリッド距離を計算することができます。
import numpy as np
np.linalg.norm(p - q)- p : 点1の座標位置の配列
- q : 点2の座標位置の配列
2次元空間のユークリッド距離の計算方法【numPyを使う方法】
linalg.norm()を使って、2次元空間のユークリッド距離を計算するpyhonのコードは以下になります。
2次元空間のユークリッド距離を計算するpythonコードの例
import numpy as np
# 2つの点p, qの座標位置の配列を定義
p = np.array([1, 3])
q = np.array([4, 7])
# 2点間のユークリッド距離を計算する
dist = np.linalg.norm(p - q)
print(dist)
# 出力結果:5.0高次元空間のユークリッド距離を計算方法【numPyを使う方法】
linalg.norm()を使って、2つの点pとqの座標位置の配列を高次元配列にすることで、より高次元空間でもユークリッド距離を簡単に計算できます。
3次元空間のユークリッド距離を計算するpythonコードの例
import numpy as np
# 2つの点p, qの座標位置の配列を定義
p = np.array([1, 3, 7])
q = np.array([4, 7, 10])
# 2点間のユークリッド距離を計算する
dist = np.linalg.norm(p - q)
print(dist)
# 出力結果:5.830951894845301配列を4次元、5次元としていくことで、より高次元空間のユークリッド距離を計算することができます。
ユークリッド距離の計算【SciPyを使う方法】
使用するSciPyの関数
次の構文で、ユークリッド距離を計算することができます。
from scipy.spatial import distance
dist = distance.euclidean(p, q)- p : 点1の座標位置の配列
- q : 点2の座標位置の配列
2次元配列のユークリッド距離の計算方法【SciPyを使う方法】
distance.euclidean()を使って、2次元空間のユークリッド距離を計算するpyhonのコードは以下になります。
2次元空間のユークリッド距離を計算するpythonコードの例
from scipy.spatial import distance
# 2つの点p, qの座標位置の配列を定義
p = [1, 3]
q = [4, 7]
# 2点間のユークリッド距離を計算する
dist = distance.euclidean(p, q)
print(dist)
# 結果:5.0高次元空間のユークリッド距離を計算方法【SciPyを使う方法】
SciPyもnumPyと同様に、2つの点pとqの座標位置の配列を高次元配列にすることで、より高次元空間でもユークリッド距離を簡単に計算できます。
3次元空間のユークリッド距離を計算するpythonコードの例
from scipy.spatial import distance
# 2つの点p, qの座標位置の配列を定義
p = [1, 3, 7]
q = [4, 7, 10]
# 2点間のユークリッド距離を計算する
dist = distance.euclidean(p, q)
print(dist)
# 結果:5.830951894845301基本的に使用する関数は違くてもnumPyもSciPyも同様の方法で、ユークリッド距離を計算できます。
“最後に” ユークリッド距離をPythonで学ぼう| まとめ
今回は、Pythonを用いたユークリッド距離の計算方法について解説しました。
ユークリッド距離は2点間の直線距離を計算するための基本的な手法であり、ユークリッド距離を理解することで、データ分析や機械学習などの分野でより高度な処理が可能になります。
本記事により、Pythonを使ってユークリッド距離を計算する方法を習得し、今後のデータ分析や機械学習の研究に役立てましょう!
最後まで、お付き合いいただきまして、ありがとうございました。





